

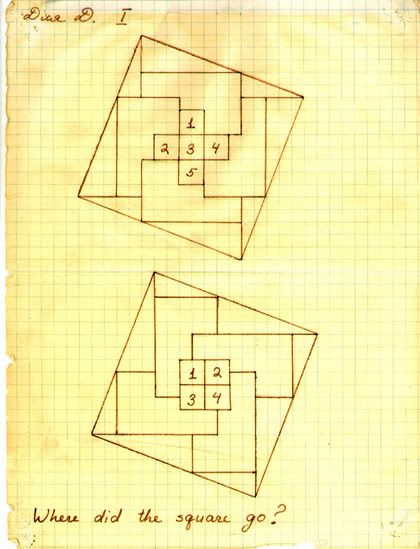
Вопрос к тем, кому нет необходимости срочно бежать повторять мат.часть: Как так? В чем тут фишка?









 )!
)!

 ))) очень сильно смеялась
))) очень сильно смеялась 







 . А всё остальное - считай, плод несовершенного изготовления деревяшек и твоего несовершенного зрения
. А всё остальное - считай, плод несовершенного изготовления деревяшек и твоего несовершенного зрения  . Я тебя уверяю - это не квадрат, потому что гиппотенузы этих треугольников никаким образом не параллельны, а расположены под ненулевым углом, не делящимся на 180 (в градусах). А как тут квадратный сантиметр набегает - ну это просто, это примерно как один клерк в банке крал с каждой сделки по 25 центов и накопил где-то миллион долларов
. Я тебя уверяю - это не квадрат, потому что гиппотенузы этих треугольников никаким образом не параллельны, а расположены под ненулевым углом, не делящимся на 180 (в градусах). А как тут квадратный сантиметр набегает - ну это просто, это примерно как один клерк в банке крал с каждой сделки по 25 центов и накопил где-то миллион долларов  .
.








Тема такая: квадратик изчез, "патамучта съибался" =))
Вывод: "плохой квадратик", т.к. нормальные квадратики так не поступают ))))))
п.с.: прошу простить, писал в опьянении..